Bit Manipulation
Bit
- 位(bit):又名比特,表示二进制位,是计算中内部数据储存的最小单位。一个二进制位只能表示 0 和 1 两种状态。
- 字节(byte):计算机中处理数据的基本单位。一个字节等于八位(1Byte = 8bit)
- 字(word):计算机进行数据处理时,一次存取、加工和传送的数据长度。在常见的计算机编码格式下,一个字等于两个字节(十六位)(1word = 2Byte = 16bit)
快速幂算法
时间复杂度$O(log\ n)$
JAVA
public long fastPowerMode(long basenumber, int exponent) { long res = 1; for (; exponent > 0; exponent >>= 1) { if (exponent % 2 == 1) { res = (res * basenumber) } basenumber = (basenumber * basenumber); } return res;}JAVA
public long fastPowerMode(long basenumber, int exponent, int mod) { long res = 1; for (; exponent > 0; exponent >>= 1) { if (exponent % 2 == 1) { res = (res * basenumber) % mod; } basenumber = (basenumber * basenumber) % mod; } return res;}求>=cap 中 2 的幂的最小值
JAVA
static final int tableSizeFor(int cap) { int n = cap - 1; n |= n >>> 1; n |= n >>> 2; n |= n >>> 4; n |= n >>> 8; n |= n >>> 16; return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1; }$$
\begin{align*}
&例如cap = 10 = (1010)_2 \\
&n = cap - 1 = (1001)_2 \\
&大于n的最小2的幂为 (10000)_2,故只需要将n各位全部置为1之后再加1即可
\end{align*}
$$
2 的整数次幂的数,最高位是 1,其余位都是 0,例如 16 的二进制位:10000,那么 15 就是1111,所以反复或的操作就是不断地把每个位数都变成 1,最后+1 就变成了最近的二的整数次幂的数
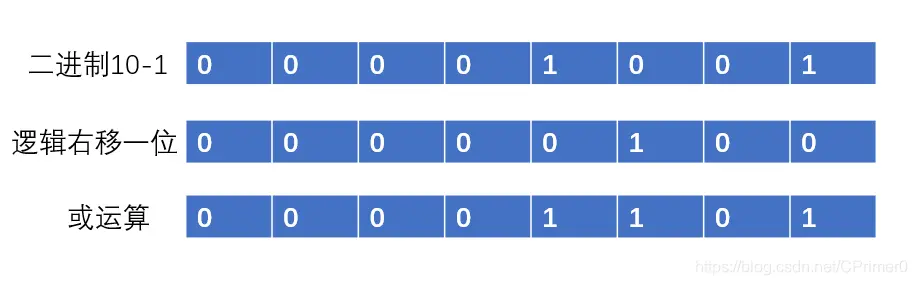
第一次或操作:向右移动一位,最高有效位 1 也会向右移动一位,我们知道或操作有 1 就变成 1,所以最高两位有效位都会变成 1
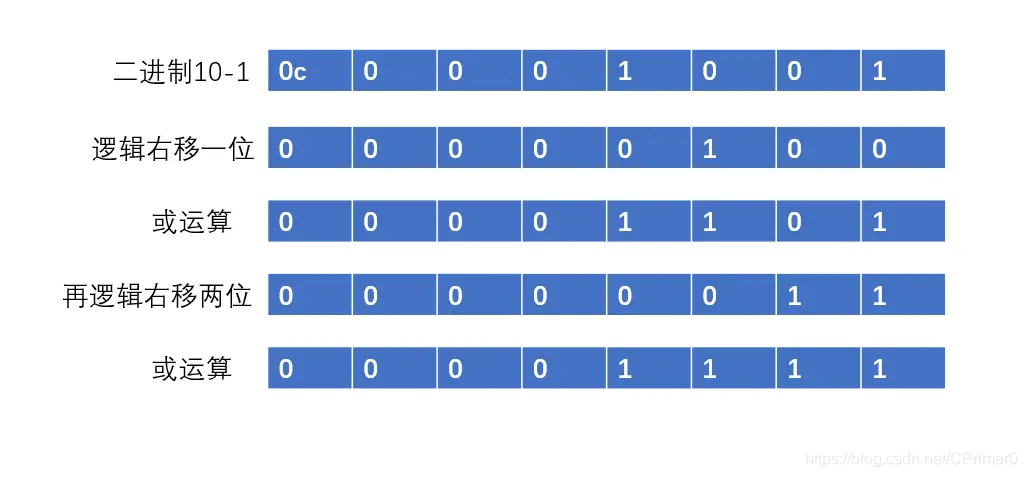
第二次或操作:当再向右移动两位,相当于把第一步的高两位向后移动两位,所以或运算后,四位都是 1
此时已经完成操作了,再移动结果不改变,最多移动 16 位,是因为 int4 个子节,32 位,最多移动高 16 位到低 16 位就能完成操作
所以当位运算操作完之后,(n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;这里如果不超过最大值就返回 n+1,例子中返回 15+1 = 16
Bit Manipulation