数据链路层 Datalink Layer Ⅰ

Introduction to the Link Layer

节点 Node 运行链路层协议的任何设备
链路 Link 指从一个结点到相邻结点的一段物理线路，中间没有其他的交换结点
数据链路 Data Link 把实现通信协议的硬件和软件加到链路上，就构成了数据链路
帧 Frame 是数据链路层的传输单位，由数据部分和控制部分组成

The Service Provide by the Link Layer

链路层提供的服务可能包括以下几点

• Framing 封装成帧。将数据报封装成数据帧，增加相应的头部和尾部信息

• Link access 链路接入

• Reliable delivery 可靠交付。在相邻节点之间可靠传输数据帧，当传输链路是比特错误率很低的链路时，例如光纤和双绞线，很少使用可靠数据传输机制；而在无线链路这样的高比特错误率链路时，通常会增加可靠数据传输机制。

• Error detection and correction 差错检测和纠正。接收方需要检测收到的数据帧是否发生比特错误，如果检测到错误，则可以通知发送方重传数据帧或直接丢弃该数据帧。或接收方可以对比特错误进行标识和纠正，不需要请求重传数据帧。

• flow control 流量控制机制，用于控制发送节点向接收节点发送数据帧的频率。避免过快发送，使接收节点的缓冲区溢出。

• half-duplex and full-duplex 半双工和全双工。半双工或全双工的数据传输，在半双工模式下，链路的两个节点都可以发送数据帧，但不能同时发送。

局域网属于数据链路层
局域网虽然是个网络。但我们并不把局域网放在网络层中讨论。这是因为在网络层要讨论的是多个网络互连的问题，是讨论分组怎么从一个网络，通过路由器，转发到另一个网络。
而在同一个局域网中，分组怎么从一台主机传送到另一台主机，但并不经过路由器转发。从整个互联网来看，局域网仍属于数据链路层的范围

Where Is the Link Layer Implemented?

链路层可以在主机和网络设备(路由器)上实现，在主机上，链路层的主体部分在网络适配器（network adapter）上实现，也称为网络接口卡（Network Interface Card，NIC），一个典型的主机体系结构如下图所示：

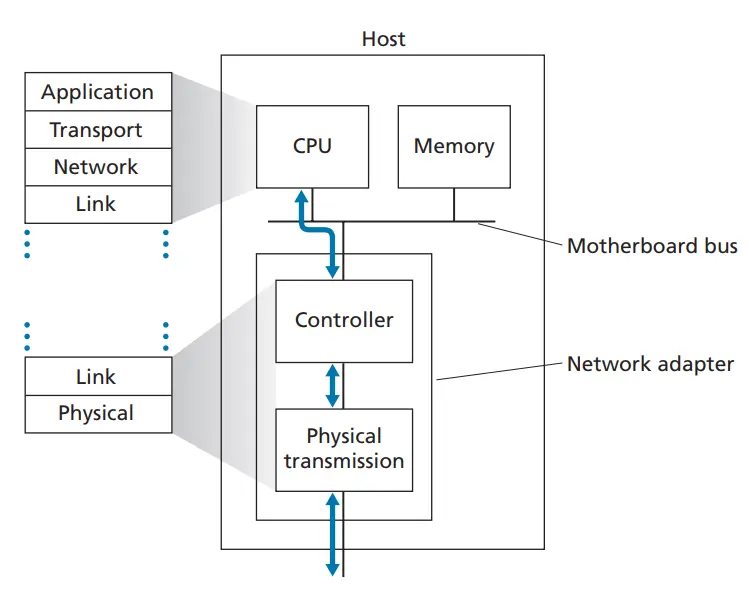
在发送方，链路层控制器将数据报封装成数据帧，增加差错检测比特，可靠数据传输，流量控制等机制。
在接收方，链路层控制器接收数据帧，执行差错检测、可靠数据传输、流量控制等机制，最后从数据帧中抽取数据报，递交给上层。

数据链路层使用的信道
数据链路层属于计算机网路的低层。数据链路层使用的信道主要有以下两种类型：

• 点对点信道 point to point link
• 广播信道 broadcast link
  

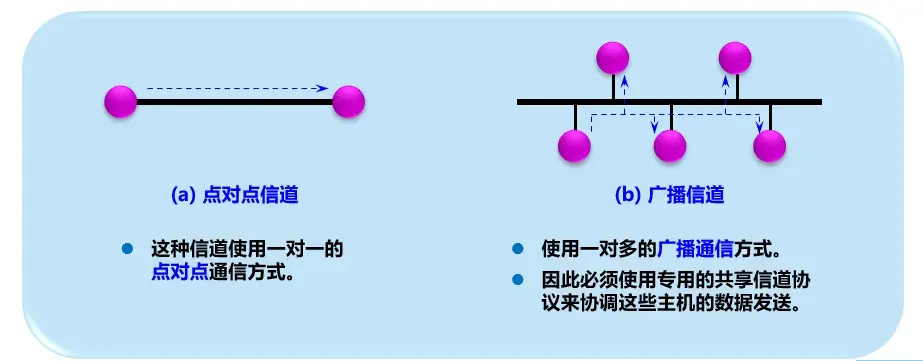
数据链路层的三个重要问题

• 封装成帧 Framing 在数据前后添加帧头和帧尾，用于标识帧的开始和结束
• 差错检测 Error Detection 传输过程中可能会产生比特差错,通过帧尾中的检错码检测帧中是否有误码
• 可靠传输 Reliable delivery 如果接收方收到有误码的帧，会丢弃这个帧。如果数据链路层向其上层提供的是不可靠服务，那么丢弃后不会再有更多措施;如果是可靠服务则需要其他措施，来确保接收方主机重新收到帧的正确副本

对于广播信道的数据链路层,还有以下问题需解决

• 确认帧的接收 Link Access 主机如何确认帧是发送给自己的? 可以通过 MAC 地址来确认
• 数据碰撞 Collide 如果两个主机同时发送数据，可能会发生数据碰撞

随着技术的发展，交换技术的成熟，在有线（局域网）领域使用点对点链路和链路层交换机的交换式局域网取代了共享式局域网;在无线局域网中仍然使用的是共享信道技术

封装成帧 Framing

封装与解包 Encapsulation&De-encapsulation

封装(Encapsulation)是低层协议从高层协议接收数据，然后将数据放入其帧的数据部分的过程。因此，封装是把一种数据包封装另一种数据包的过程。
解包(Decapsulation)与之相反,高层协议从低层协议接收数据，然后逐层将数据从帧的数据部分取出的过程。

Generally, Encapsulation is a process by which a lower-layer protocol receives data from a higher-layer protocol and then places the data into the data portion of its frame. Thus, encapsulation is the process of enclosing one type of packet using another type of packet.

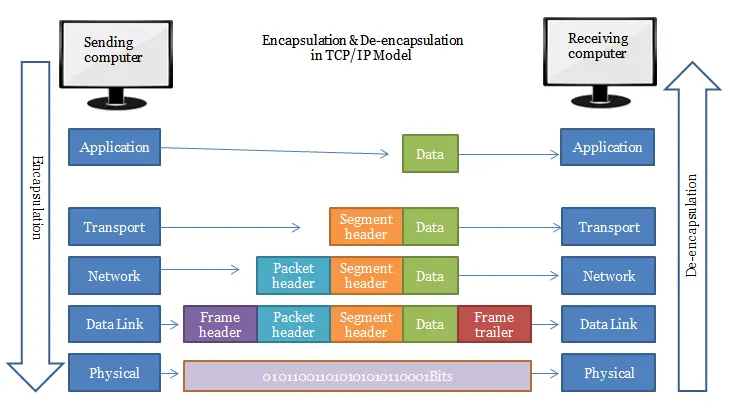
封装成帧(Framing)指数据链路层接受上层交付的协议数据单元,并为其添加帧头和帧尾,使之成为帧的过程

发送方的数据链路层将上层交付下来的协议数据单元封装成帧后，通过物理层将构成帧的 bits 转换成电信号交给传输媒体，接收方的数据链路层再从物理层交付的比特流中提取出 frames
解包过程如何提取 frames?

• PPP 帧 依据帧头和帧尾的标志符确定帧的开始和结束(帧定界)从而提取出 frames
• 以太网 V2 的 MAC 帧 根据前导码(1 字节的帧开始定界符,7 字节的前同步码)来定界,帧间间隔为 96bit 的时间
  • 前同步码:作用是使接收方的时钟与发送方的时钟同步
  • 帧开始定界符:标志帧的开始
  • 以太网规定帧间间隔为 96bit 的时间,因此 MAC 帧不需要帧结束定界符

透明传输 Transparent transmission

透明传输是指不管所传数据是什么样的比特组合，都应当能够在链路上传送。因此，链路层就“看不见”有什么妨碍数据传输的东西。

当所传数据中的比特组合恰巧与某一个控制信息完全一样时，就必须采取适当的措施，使收方不会将这样的数据误认为是某种控制信息。这样才能保证数据链路层的传输是透明的。
解决办法

• 字符填充/字节填充
  • 发送方扫描数据,当数据中出现与帧定界符相同的比特串时,在其前面插入转义字符 ESC;
  • 接受方将遇到的第一个帧定界符认为是帧的开始
  • 遇到转义字符时,则知道后面的比特串虽与帧定界符相同,但并非帧定界符而是数据,因此剔除转义字符 ESC 然后将其后的字符作为数据处理
  • 当再次遇到帧定界符时,认为帧结束
    
    ps:遇到与转移字符相同的比特串时,则在转义字符前面再插入转义字符
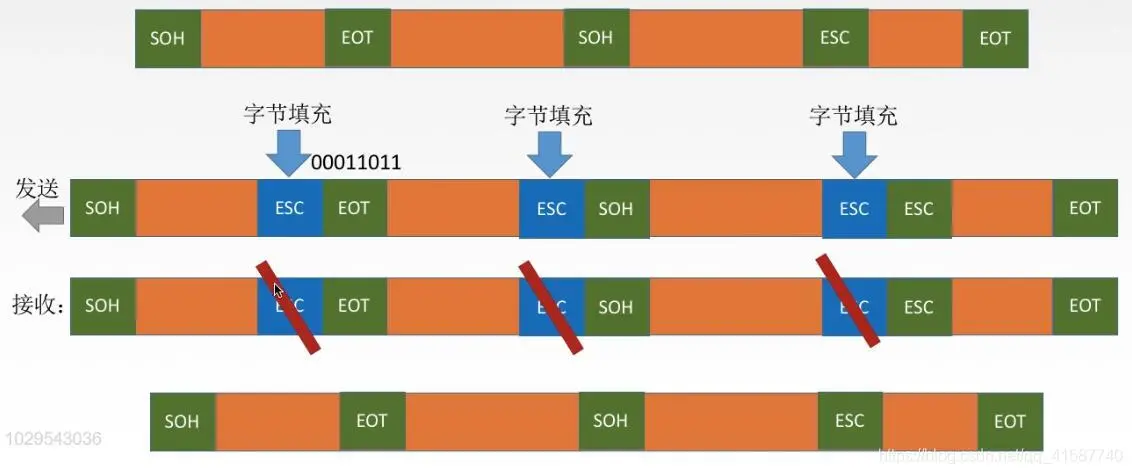
• 比特填充
  

为了提高帧的传输效率，应当使帧的数据部分的长度尽可能大些。
考虑到差错控制等多种因素，每一种数据链路层协议都规定了帧的数据部分的长度上限，即最大传送单元 MTU(Maximum Transfer Unit)

差错检测 Error Detection

差错检测的基本概念

实际的通信链路都不是理想的，比特在传输过程中可能会产生差错：1可能会变成0 ，而0也可能变成1,这称为比特差错。
在一段时间内，传输错误的比特占所传输比特总数的比率称为误码率BER(Bit Error Rate)
使用差错检测码来检测数据在传输过程中是否产生了比特差错，是数据链路层所要解决的重要问题之一
帧校验序列 FCS(Frame Check Sequence)是差错检测码的一种，用于检测帧中是否有误码,通常使用循环冗余校验 CRC来计算 FCS

差错检测和纠正技术不能保证接收方检测到所有的比特差错，即可能出现未检测到的比特差错，而接收方并未发现。
实际中选择一个合适的差错检测方案使未检测到的情况发生的概率很小即可。差错检测和纠错技术越复杂，通常检错性能越好，但是开销更大。

奇偶校验 Parity Check

一比特奇偶校验 One-Dimensional Parity Check

奇偶校验在待发送的数据后面添加 1 位奇偶校验位，使整个数据（包括所添加的校验位在内）中1的个数为奇数（奇校验）或偶数（偶校验）。
如果有奇数个bit 发生误码，则奇偶性发生变化，可以检查出误码；
如果有偶数个bit 发生误码，则奇偶性不发生变化，不能检查出误码（漏检）

在一比特奇偶校验中：

• 可以查出任意奇数个错误，但不能发现偶数个错误。
• 若比特差错概率很小，差错独立发生，一比特奇偶校验可满足要求。
• 若差错集中一起“突发”（突发差错），一帧中未检测到的差错的概率达到 50%。

二维奇偶校验 Two-Dimensional Parity Check

假设传输信息 D 有 d 位，在偶校验方案中，会增加一个附加的比特，使得这 d+1 个比特中 1 的总数是偶数。由于普通的奇偶校验方式检错能力有限，所以产生了二维的奇偶校验。D 中的 d 个比特被划分为 i 行 j 列，对每行每列计算奇偶值，产生的 i+j+1 个奇偶比特构成了链路层帧的差错检测比特。

我们来看一下二维偶校验的例子。
假设要发送的数据是 10101 11110 01110，共 15 比特，
我们首先将其按 5 比特一组划分为 5 列 3 行，然后进行偶校验，

第一行有 3 个 1，因此第一行的校验位为 1，
第二行有 4 个 1，因此第二行的校验位为 0，
第三行有 3 个 1，因此第三行的校验位为 1，
假设在传输过程中，有一个比特错误，例如第二行第二列的 1 发生了翻转，变为了 0，
在接收方进行检验时，会发现第二行的校验位不对，以及第二列的校验位不对，这样一交叉就会发现，第二行第二列的比特发生错误。
因此二维奇偶校验可以检测并纠正单个比特差错；能够检测分组中任意两个比特的差错。

特点：

• 可以检测并纠正单个比特差错（数据或校验位中）
• 能够检测(但不能纠正)分组中任意两个比特的差错

校验和 Checksumming Method

因特网检验和 Internet checksum基于这种方法，即数据的字节作为 16 比特的整数对待并求和。

• 发送方：
  • 将数据的每两个字节当作一个 16 位的整数，可分成若干整数；
  • 将所有 16 位的整数求和；
  • 对得到的和逐位取反，作为 Checksum，放在报文段首部，一起发送。
• 接收方：
  • 对接收到的信息 (包括检查和)按与发送方相同的方法求和。
  • 全“1”：收到的数据无差错；
  • 其中有“0”：收到的数据出现差错。

特点

分组开销小：检查和位数比较少；
差错检测能力弱：
适用于运输层（差错检测用软件实现，检查和方法简单、快速）。
链路层的差错检测由适配器中专用的硬件实现，采用更强的 CRC 方法。

Internet_Checksum

循环冗余校验 Cyclical Redundancy Check

CRC（Cyclic Redundancy Check） 是计算机网络中常用的一种 差错检测编码方法，又称为 多项式编码。它通过将二进制比特串看作一个二进制多项式（每一位为该项系数，取值为 0 或 1）进行模 2 运算，从而实现高效可靠的错误检测。它能检测小于 r+1 位的突发差错、任何奇数个差错

设发送方要发送的数据为D，发送方与接收方事先约定一个 生成多项式 G（r+1 位），约定G的最高位为 1。

• 发送方：
  1. 在 D 的末尾添加 r 个 0，得到 D × 2^r（相当于比特串左移 r 位）。
  2. 用 D × 2^r 模 2 除以 G，得到余数 R，即$$D \times 2^r \oplus R = nG$$
  3. 将余数 R 添加到原始数据 D 的末尾，形成新的比特串 DR，如果 R 的长度不足 r 个 bit 则在高位补 0，得到的DG满足条件DR / G余数为 0，发送 DR 给接收方。
• 接收方：
  1. 接收到 DR 后，用 G 对其进行模 2 除法。
  2. 如果余数为 0，则认为传输无误，去除末尾 r 位得到原始数据 D。
  3. 如果余数不为 0，则说明数据在传输过程中发生了差错。

余数 R 是否会超过 r 个 Bit？

在除法运算中，被除数 = 除数 × 商 + 余数，且余数 < 除数，对于 CRC 中的模 2 除法也是如此：
$$D \times 2^r = G \times Q + R$$

其中：
$D \times 2^r$ 是被除数（d+r 位）,$G$ 是除数（r+1 位）,$Q$ 是商,$R$ 是余数

根据除法的基本性质，余数必须小于除数, 即$R < G$，又由于生成多项式 G 是 r+1 位的二进制数（最高位为 1），所以：

• G 的最小值是 $2^r$（二进制：100…0，共 r+1 位）
• G 的最大值是 $2^{r+1}-1$（二进制：111…1，共 r+1 位）

因此余数 R 满足$0 \leq R \leq 2^r-1$，即其长度不可能超过 r 个 Bit

DR 可以被 G 模 2 运算整除吗？

在上面得到这样的关系：$$D \times 2^r \oplus R = nG$$

由于 DR 中的 R 被填充成 r 位，所以有

$$DR = D \times 2^r + R$$

而在模 2 运算中，加法等价于异或运算：

$$DR = D \times 2^r \oplus R$$

Conclusion

差错检测方法比较

• 奇偶校验能力最弱，CRC 校验能力最强。
• 奇偶校验通常用于简单的串口通信
• Internet 校验和通常用于网络层及其之上的层次，要求简单快速的软件实现方式
• CRC 通常应用于链路层，一般由适配器硬件实现

检错纠错的基本原理

• 为了校错和纠错，我们在发送方对信息位进行编码，而在接收方进行解码，以还原信息。编码的原理是增加冗余信息检验位。
• 假设要传送的信息为 m 位，校验位为 r 位，则编码的总长度为 m ＋ r 位。所谓编码就是把 m 位信息码映射为 n =m ＋ r 位的编码。
• m 位信息仅有 $2^m$ 种信息码，而 m ＋ r 位则有 $2^{m+r}$ 种编码。因此把 m ＋ r 位的编码分为两大类：有效码和无效码，有效码指与信息码有一一映射关系的编码，所以有效码有 $2^m$ 个。而其余的编码则称之为无效码，无效码共有 $2^n-2m= 2^{m+r}-2m =(2^r-1)2m$ 个。
• 发方进行编码就是把信息码映射为有效码
• 由于信道有错，有效码在传送过程中有可能变成了无效码
• 当接收方收到信道传来的编码信息时，首先判断它是有效码还是无效码。
  • 如果是有效码则通过逆映射关系，解码出原信息
  • 如果是无效码，则认为出了错，这就是检验出错误
• 假设通过无效码能够分析出它是由哪一个有效码出错而来的，从而找出原信息码，这就称为纠错（编码）
• 如果信道出错使一个有效码变成另一个有效码，则收方检不出错

但纠错码的开销比较大，在计算机网络中较少使用。
循环冗余校验有很好的检错能力,漏检率非常低，虽然计算比较复杂，但非常易于用硬件实现，因此被广泛应用于数据链路层。在计算机网络中通常采用检错重传方式来纠正传输中的差错，或者仅仅是丢弃检测到差错的帧，这取决于数据链路层向其上层提供的是可靠传输服务还是不可靠传输服务。

可靠传输 Reliable Transmission

Overview

可能发送的差错

• 比特错误 使用差错检测技术（例如循环冗余校验 CRC，接收方的数据链路层就可检测出帧在传输过程中是否产生了误码（比特错误）。一般情况下，有线链路的误码率比较低，为了减小开销，井不要求数据链路层向上提供可靠传输服务。即使出现了误码，可靠传输的问题由其上层处理。无线链路易受干扰，误码率比较高，因此要求数据链路层必须向上层提供可靠传输服务。
• 分组丢失 路由器输入队列快满了，主动丢弃收到的分组
• 分组时序 数据并未按照发送顺序依次到达接收端
• 分组重复 由于某些原因，有些分组在网络中滞留了，没有及时到达接收端，这可能会造成发送端对该分组的超时重发，重发的分组到达接收端，但一段时间后，滞留在网络的分组也到达了接收端，这就造成分组重复的传输差错

三种可靠传输方式

• 停止等待协议 SW
• 回退 N 帧协议 GBN
• 选择重传协议 SR

停止等待协议 Stop-and-Wait Protocol

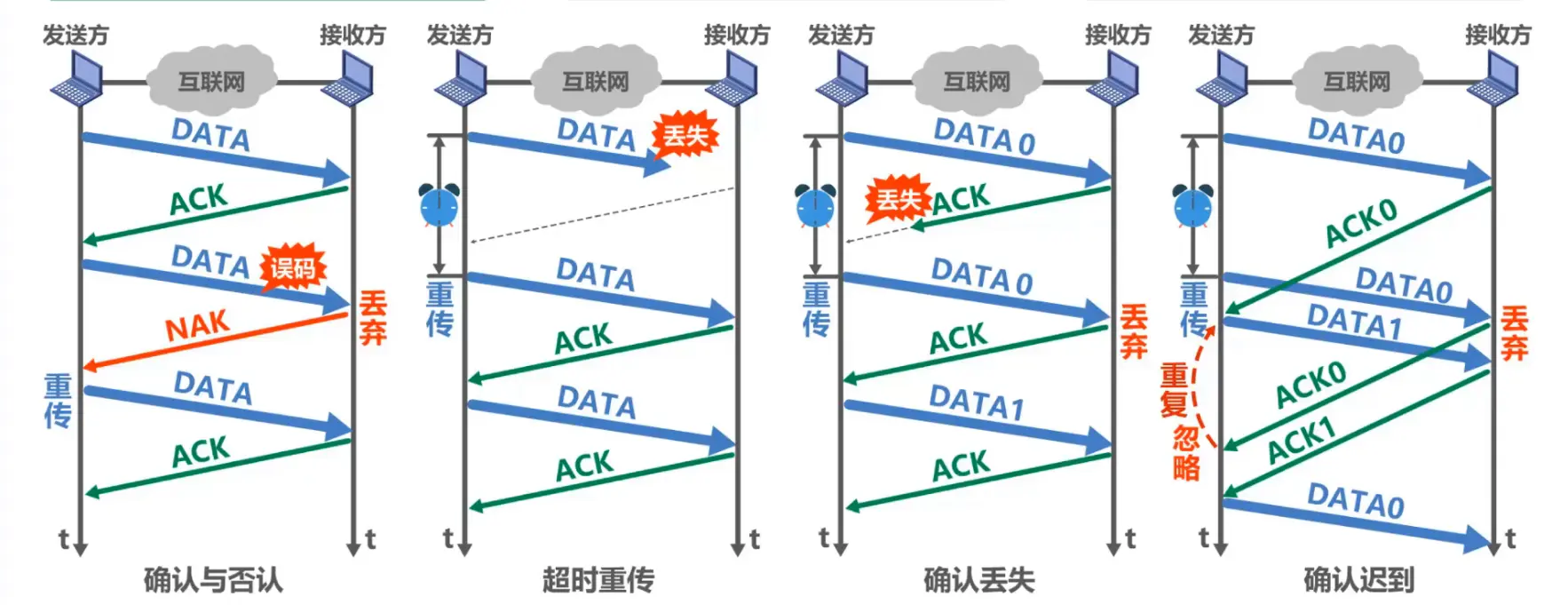
确认与否认

首先，每次发送方都只发一个数据分组，接收方对数据分组进行差错检测，检验是否有误码;

如果没有误码，接收方发送ACK确认分组,发送方收到ACK确认分组后，发送方才能发送下一个数据分组。

如果有误码,接收方发送NAK否认分组并丢弃当前分组,发送方收到NAK否认分组后，重发数据分组。

超时重传

接收方收不到数据分组，就不会发送ACK或NAK。如果不采取其他措施，发送方就会一直处于等待接收方ACK或NAK的状态。数据分组在传输过程中有可能遇到已经满了的路由器等情况，此时路由器会丢失该分组，如此便会产生数据分组被丢失，发送方等不到接收方的ACK或者NAK,导致发送方陷入等待状态。

为解决该问题，可以在发送方发送完一个数据分组时，启动一个超时计时器。若到了超时计时器所设置的重传时间而发送方仍收不到接收方的任何ACK或NAK，则重传原来的数据分组，这就叫做超时重传。

超时计时器设置的重传时间应仔细选择。一般可将重传时间选为略大于从发送方到接收方的平均往返时间;在数据链路层点对点的往返时间比较确定，重传时间比较容易设定。然而在运输层，由于端到端往返时间非常不确定，设置合适的重传时间有时并不容易。

确认丢失

实际过程中,接收方发送的ACK或NAK也可能会丢失,发送方收不到接收方的ACK或NAK，触发超时计时器,会重传数据分组。如果接收方成功接收了数据分组，但发送ACK的分组丢失了，发送方会重传数据分组，这样会导致接收方收到重复的数据分组。

为解决该问题,我们用一个比特位给每个数据分组一个序号（0 或 1），当重新传输数据分组的时候，接收方检测到这个数据分组的序号,如果刚才的数据分组的序号相同就丢弃该数据分组，否则接收该数据分组。然后发送ACK确认分组。

这里为什么可以只用0和1呢，主要还是因为停止等待协议的特性，即每发送完一个数据分组便等待发送方的ACK或NAK，只要保证每发送一个新的数据分组，其发送序号与上次发送的数居分组的序号不同就可以了，因比用一个比特来编号就够了。

确认迟到

为了让发送方能够判断所收到的ACK分组是否是重复的，需要给ACK分组编号，所用比特数量与数据分组编号所用比特数量一样。数据链路层一般不会出现ACK分组迟到的情况，因此在数据链路层实现停止．等待协议可以不用给ACK分组编号。

信道利用率

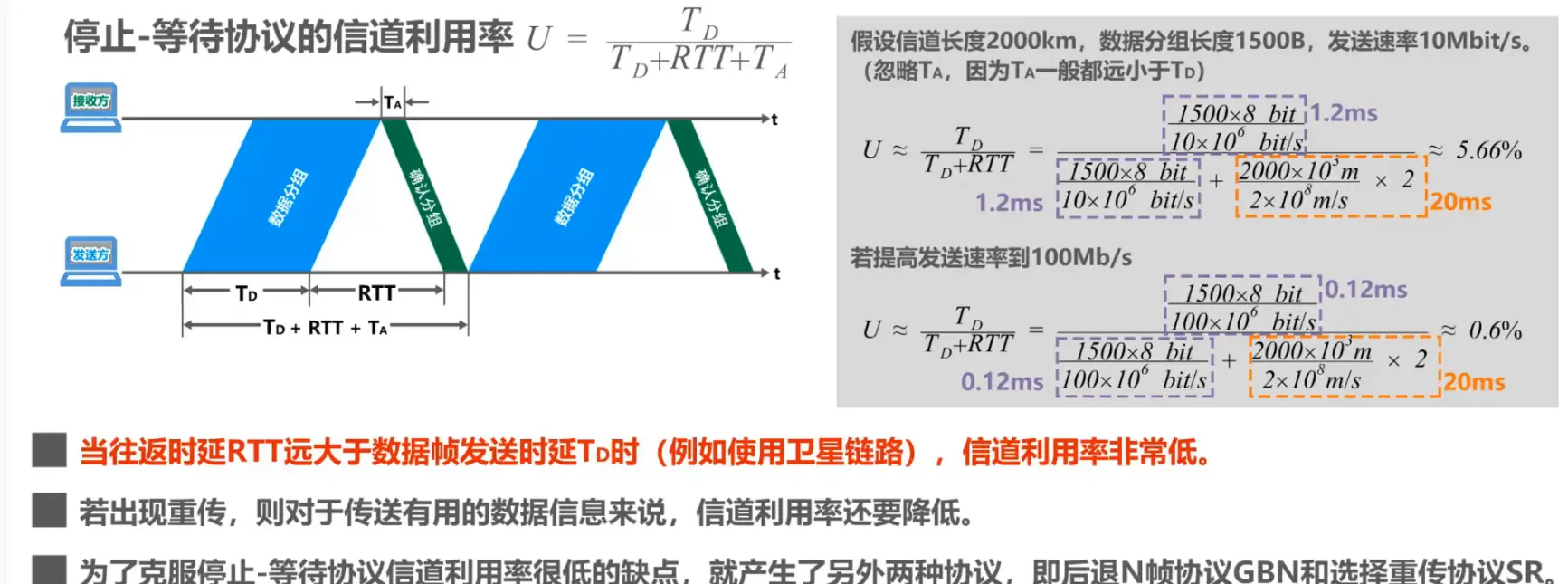
回退 N 帧协议 Go-Back-N Protocol

在停止-等待协议中，随着 RTT 的变大，信道的利用率也会变低（卫星通信），解决该问题的方法是：不以停等方式运行，允许发送方发送多个分组而无须等待确认。因为许多从发送方向接收方输送可以看成是填充到一条流水线中，故这种技术被称为流水线（pipeline），下图为停等和流水线发送示意图：

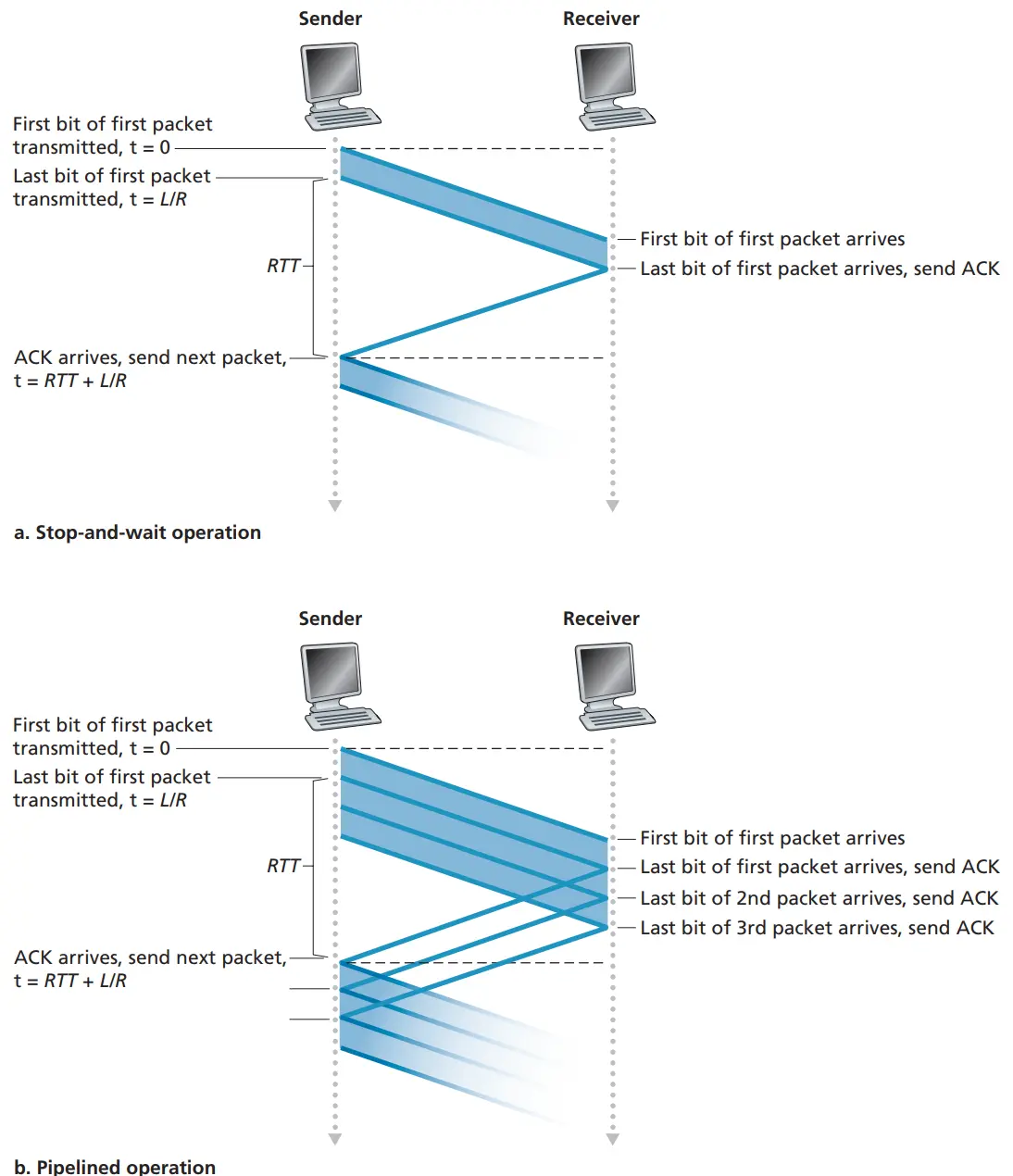
在回退 N 步协议中，将基序号（base）定义为最早未确认分组的序号，将下一个序号（nextseqnum）定义为最小的未使用序号，则将序号范围分割成如下 4 段：

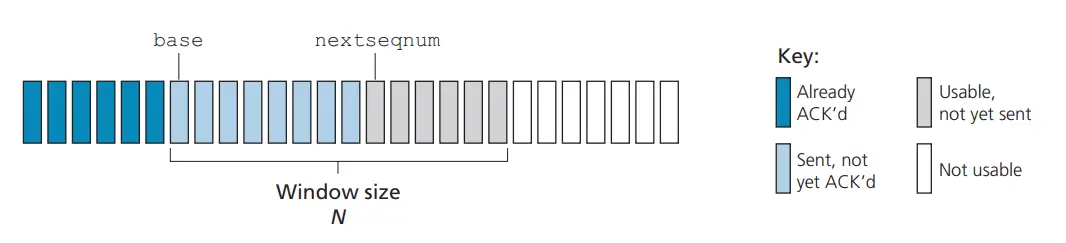
GBN 协议也常被称为滑动窗口协议(sliding-window protocol)中，窗口大小 N 决定了可以在没有确认的情况下发送的数据包的最大数量。这个窗口会随着数据包的确认而向前滑动。限制窗口大小的原因有两个，一个是流量控制，防止接收者被发送者的大量数据包淹没；另一个是 TCP 拥塞控制

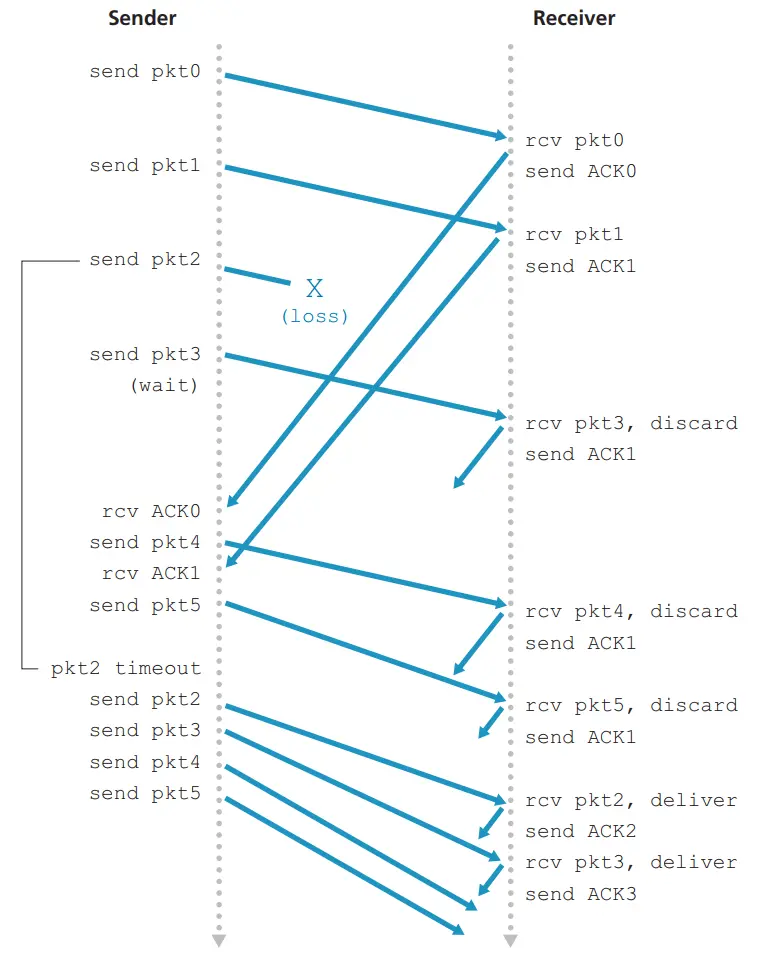
在 GBN 协议中，接收方丢弃所有失序分组。这种方法的优点是接收缓存简单，即接收方不需要缓存任何失序分组。因此，虽然发送方必须维护窗口的上下边界及 nextseqnum在该窗口的位置，但接收方需要维护的唯一信息就是下一个按序接收的分组序号。运行中的 GBN 如下图所示：

Notes

• 如果某个报文段没有被正确接收，则从这个报文段到后面的报文段都要重新发送。
• 采用累计应答的方式。例如接收端返回 ACK=3，则证明报文段 3 以及之前的报文段都被正确接收。(GBN 如何保证 3 之前的数据被正确接收了呢？在 GBN 的接收窗口$W_{R}=1$,即按顺序逐个接受数据,因此接收方只能按序接受正确到达的数据分组)
• 接收端不对失序到达的分组进行缓存。
• 回退帧协议在流水线传输的基础上利用发送窗口来限制发送方连续发送数据分组的数员，是一种连续 ARQ 协议，
• 在协议的工作过程中发送窗囗和接收窗囗不断向前滑动，因此这类协议又称为滑动圊囗协议。
• 缺点:如果发生错误，GBN 协议会丢弃后续的所有包，即使它们已经到达并且没有错误。这可能导致效率低下，特别是在通信线路质量不好的情况下

有限状态机 FSM

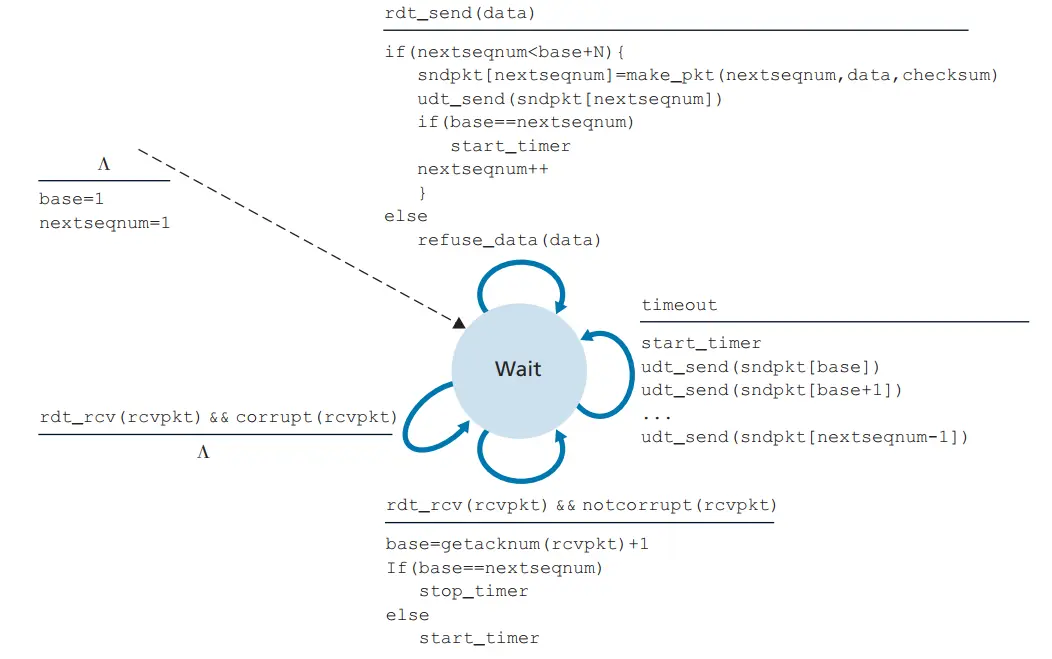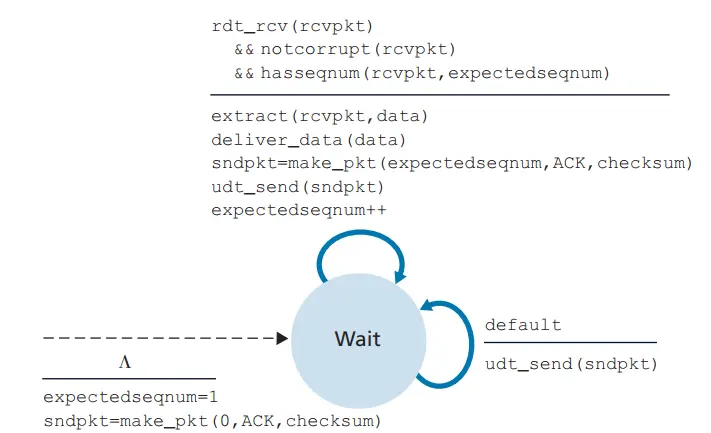选择重传协议 Selective Repeat Protocol

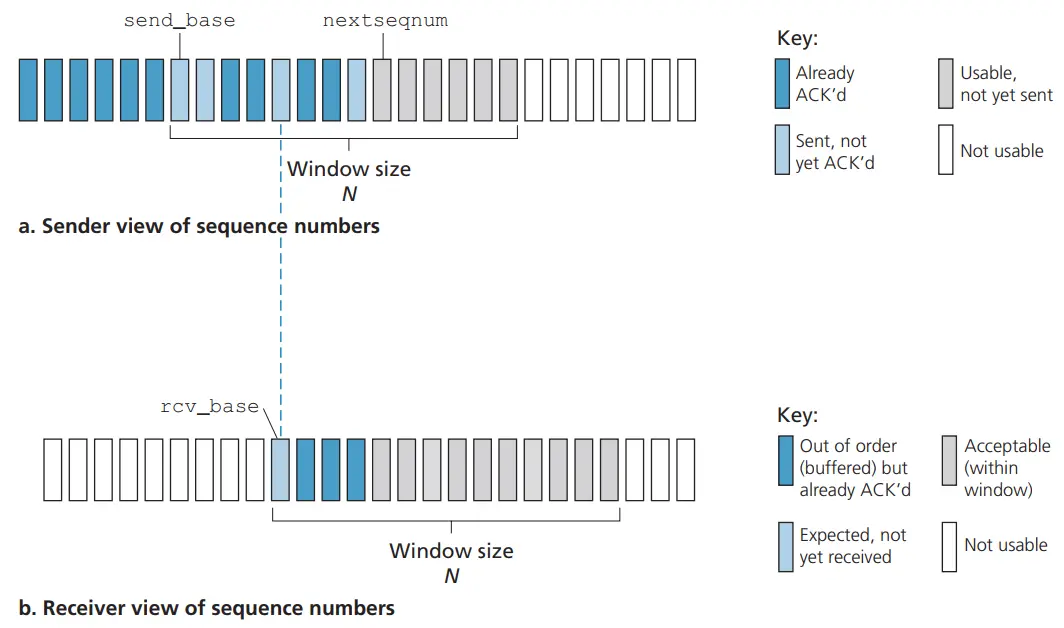
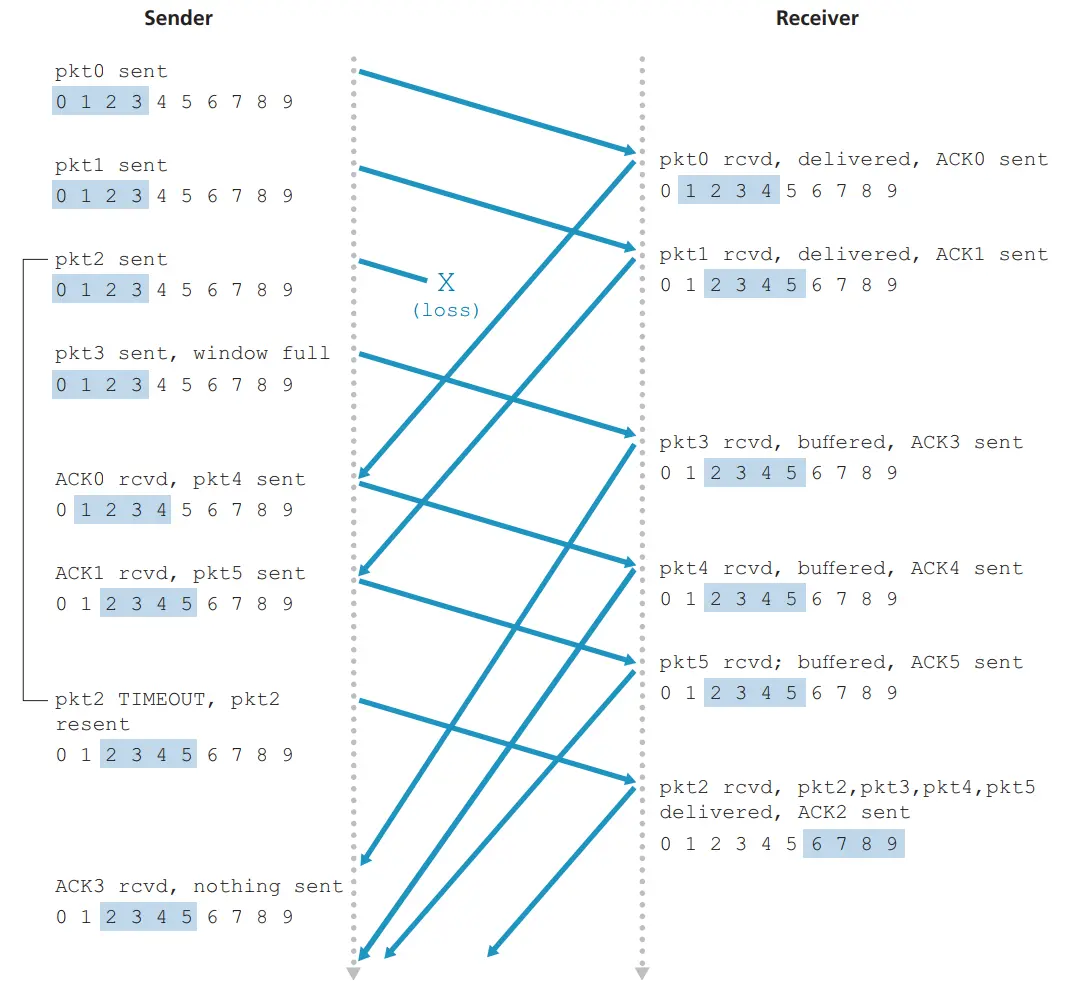
GBN 协议的接收窗口尺寸 WR 只能等于 1 ，因此接收方只能按序接收正确到达的数据分组。一个数据分组的误码会导致其后续多个数据分组不能被接收方按序接收而丢弃（尽管它们无乱序和误码）。这必然会造成发送方对这些数据分组的超时重传，显然这是对通信资源的极大浪费。为了进一步提高性能，可设法只重传出现误码的数据分组。因此，接收窗口的尺寸不应再等于 1 （而应大于 1 ）以便接收方先收下失序到达但无误码井且序号落在接收窗口内的那些数据分组，等到所缺分组收齐后再一井送交上层。这是选择重传协议。

$$
\begin{align*}
& 发送窗口尺寸W_{T}必须满足: 1 < W_{T} \lt 2^{n-1}; n为分组中的bit数 \\
& 若W_{T} = 1,则退化为停止等待协议;若W_{T} \gt 2^{n-1},则会造成接收方无法辨别新旧数据分组的问题\\
& 接收窗口尺寸W_{R}必须满足: 1 < W_{R} \leq W_{T}\\
& 若W_{R} = 1,则退化为回退 N 帧协议;W_{R} \gt W_{T}没有意义
\end{align*}
$$

Ref

www.tkn.tu-berlin.de/teaching/rn/animations/gbn_sr/
zhuanlan.zhihu.com/p/126312611
Ch5-1TransportLayer